NELINEARNOSTI U MKE
U našem prethodnom članku objasnili smo kako možemo koristiti Metodu konačnih elemenata u građevinskom inženjerstvu i zaključili smo da je MKE odličan alat za rešavanje mnogih problema u ovoj, ali i u mnogim drugim inženjerskim oblastima. Ovog puta, zaći ćemo malo dublje i pozabaviti se tipovima analiza koje možemo izvesti.
Bazična metoda u MKE je linearna analiza. A šta tačno znači “linearna” analiza? Kada je analiza sasvim linearna, sve jednačine koje softver za MKE treba da reši bile bi linearne i rezultati koje želimo da dobijemo mogli bi biti jednostavno određeni u jednom koraku iz međuzavisnosti opterećenja i inicijalne krutosti modela. Nijedan od faktora koji bi mogli narušiti tu linearnu relaciju ne bi bili uzeti u obzir – geometrija konstrukcije, svojstva materijala, oslonci koji su efektivni samo u jednom smeru, njihova delimična aktivnost itd. Međutim, u stvarnosti, konstrukcije se ne ponašaju na linearan način. Za početak, opterećenja ne deluju “odjednom“ na konstrukciju. Delovi konstrukicije bivaju deformisani pod uticajem tih opterećenja, a te deformacije dalje utiču na buduće preraspodele sila među elementima. Međuzavisnost sila i deformacija razlikuje se u zavisnosti od tipa materijala. Sve navedeno dovodi nas do nelinearnih proračuna u MKE.
Kako geometrija utiče na analizu?
Prvo ćemo objasniti kako geometrija konstrukcije utiče na analizu. Kao što smo ranije pomenuli, elementi konstrukcije će se deformisati ukoliko određena sila deluje na njih, jer ti elementi nisu potpuno kruti. Dalje, svi smo upoznati sa osnovama mehanike i sa tim kako je moment produkt sile i udaljenosti od referentne tačke objekta. Ukoliko bi referentna tačka bila u istoj ravni sa silom, ne bi došlo do pojave momenta, pa samim tim, na nedeformisanoj konstrukciji se ne bi pojavili momenati nastali usled uticaja aksijalnih sila. Budući da smo rekli da se kontrukcija uvek deformiše pod uticajem opterećenja, to bi značilo da uvek postoje momenti nastali usled dejstva aksijalnih sila tj. takozvani momenti drugog reda. To je potpuno tačno, ali ipak postoje određene situacije u kojima ih možemo ignorisati. Naravno, uvek možemo da ih izračunamo, ali ponekad će to biti nepotrebno, jer neće imati značajan uticaj na dalje rezultate. Situacije i pravila koja se tiču uzimanja u obzir momenata drugog reda u analizi i proračunu konstrukcija opisani su u većini građevinskih standarda, kao što su Evrokod, AISC, Australijski standardi itd.
A kako to proračuni momenata drugog reda utiču na MKE? Linearni pristup proračunu podrazumeva da nakon što sprovedemo proračun opterećene konstrukcije, softver jednostavno pronađe unutrašnje sile, kao što su momenti, smičuće i aksijalne sile. Takođe, dobijamo i uvid u krajnje deformacije konstrukcije, ali te deformaicije neće imati uticaj na povećanje momenta, jer je program izračunao sve unutrašnje sile na nedeformisanom sistemu. S druge strane, ako bismo se odlučili da izvedemo geometrijsku nelinearnu analizu, proračun bi bio iterativan. Opterećenja bi morala biti naneta inkrementalno, tako da sa svakim novim inkrementom dobijemo novu vrednost deformacije koja će uticati na proračun u sledećem koraku. Program će nastaviti sa iterativnim proračunom sve dok ne se ne dobije stabilan ravnotežni položaj sistema.
Materijali sa nelinearnim svojstvima
Sledeća stavka su svojstva materijala, a opisaćemo ih za slučaj materijalnog modela kostrukcionog čelika. Zamislimo čeličnu gredu koja je jednako opterećena celom svojom dužinom. Kada je opterećenje nanešeno, dolazi do ugibanja grede, a kada se opterećenje ukloni, greda će povratiti prvobitni oblik. Naravno, može se pretpostaviti da postoji određeni nivo deformacije pri kom greda nije u stanju da povrati svoj prvobitni oblik. Ovo se dešava kada čelik dostigne svoju granicu tečenja (eng. yield strength), nakon čega ulazi u plastičnu zonu svog radnog dijagrama. Sposobnost razvoja plastičnih deformacija jedna je od najvećih prednosti čelika. Kada koristimo linerani materijalni model u našem proračunu, program ne može koristiti plastičnost čelika, jer jednostavno ona ne postoji u tom modelu, budući da je nismo uzeli u obzir. Verovatno ste upoznati sa tim kako izgleda radni dijagram čelika:
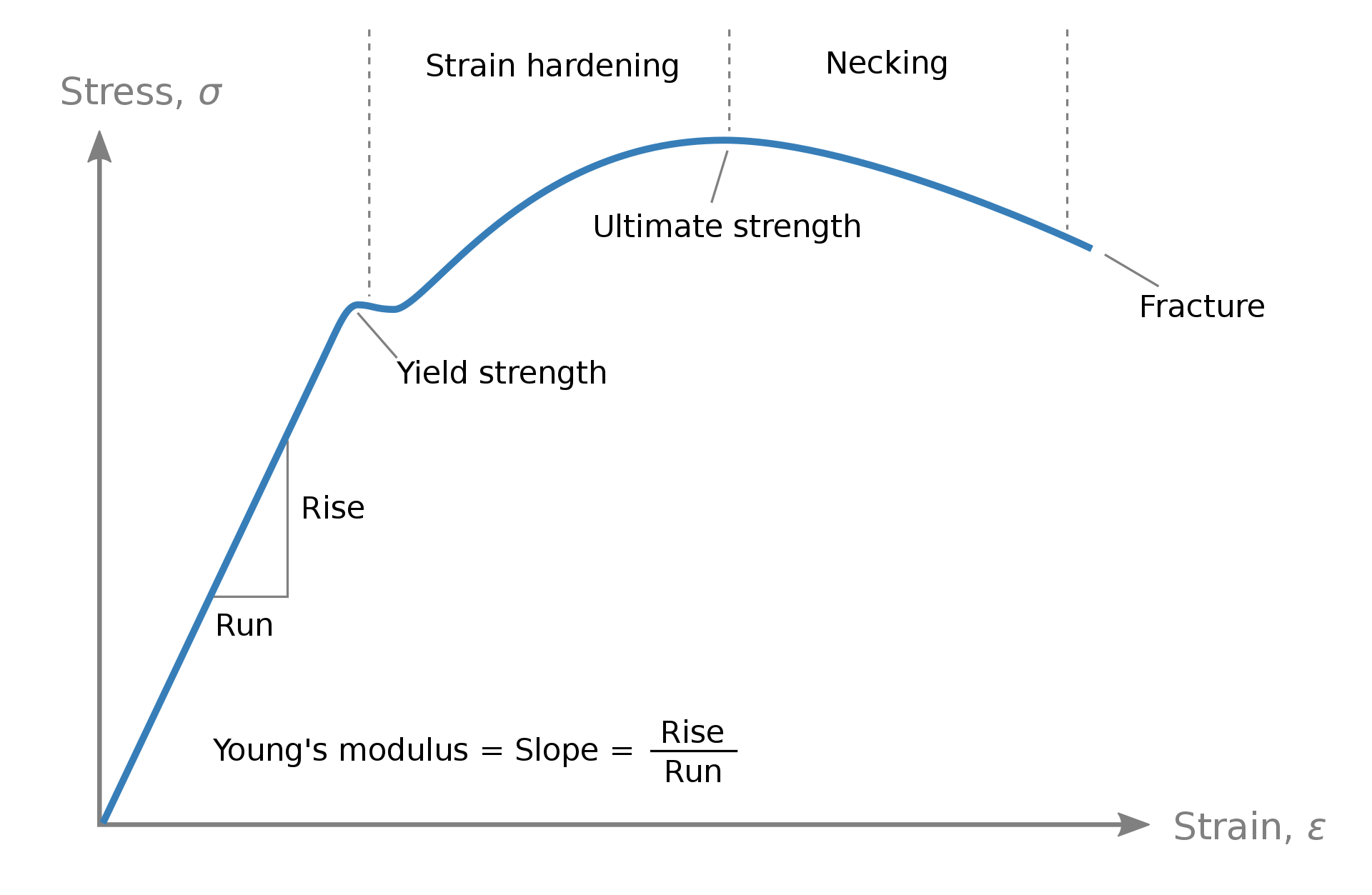
U slučaju linearnog modela, deo krive nakon tačke granice tečenja (plastični plato) ne postoji – dijagram nastavlja da bude linearan u obliku beskonačne linije. Ovo znači da ako bi opterećenje bila konstantno povećavano, napon bi se takođe povećavao u linearnoj relaciji i mogao bi ići i preko granice tečenja (do beskonačnosti). Ovo, naravno, nije moguće. Kada dilatacije (koja su rezultat deformacija nastalih pod uticajem opterećenja na elemente) u našem modelu dostignu zonu plastičnosti, naponi će se samo neznatno povećavati, dok će se poprečni presek plastifikovati. Ako želimo da uzmemo u obzir ove efekte u našem proračunu, moramo koristiti nelinearni materijalni model. Program će izračunati dilatacije na osnovu deformacija i nakon toga, odgovarajuće napone. Ako dilatacije uđu u plastičnu zonu na dijagramu, svako sledeće povećanje opterećenja će rezultovati daljim razvojem dilatacije, dok će napon ostati na granici tečenja (ili će biti nešto viši). Naravno, postoje ograničenja nivoa plastičnih dilatacija, i ona mogu biti pronađena u relevantnim standardima. Ovi standardi takođe sadrže preporuke za primenu odgovarajućeg modela nelinearnog materijala u MKE modelu, budući da je implementacija realnog radnog dijagrama u softver veoma zahtevna.
Kao projektanti čeličnih konstrukcija, objasnili smo kako se materijalna nelinearnost odražava na proračun čeličnih konstrukcija. Međutim, postoje mnogi materijali sa nelinearnim (elastičnim i/ili plastičnim) svojstvima, čije ponašanje može biti u mnogome drugačije od ponašanja čelika. Odlike ovih materijala mogu se pronaći u odgovarajućoj literaturi ili se mogu otkriti u okviru eksperimentalnih laboratorijskih testova.
Nelinearnosti vezane za tipove elemanata i oslanjanje
Dalje, nelinearnosti mogu da se odnose na uslove oslanjanja i tipove elemenata. Možemo postaviti oslonce u našem modelu tako da budu neefektivni na pritisak ili zatezanje, možemo uključiti trenje ili dozvoljena pomeranja (proklizavanja) oslonaca. Dobar primer za neefektivnost oslonca je sprečavanje pomeranja temeljne ploče u vertikalnom pravcu. Tlo (pretpostavimo čvrstvo stenovito tlo za potrebe ovog primera) ispod temelja sprečava njegova pomeranja na dole (u pravcu gravitacije), a samim time i pomeranja cele konstrukcije. S druge strane, tlo ne sprečava odizanja konstrukcije (niti može preneti zatežuće sile u svom kontaktu sa temeljom). U ovom slučaju, odgovarajući način za zadavanje oslonca temeljnoj ploči bi bilo kreiranje površinskog oslonca koji je neefektivan na zatezanje (ili odizanje). Ili zamislimo čeličnu gredu prosto oslonjenu na dva zida, bez ikakvog ankerisanja. Ni ovde nemamo mogućnost da sprečimo odizanje grede budući da nije fiksirana za zid. Stoga, trebamo da kreiramo oslonce na krajevima greda koje će se odlikovati pomenutom nelinearnošću. Ali, šta se dešava sa horizontalnim pomeranjem? Neko bi mogao reći da greda nije oslonjena u horizontalnom pravcu, ali zahvaljujući trenju ipak imamo određeni otpor pomeranju. Trenje može biti dodeljeno kao nelinearnost osloncu ili može biti modelirano kao ulazni parametar za kontakt. Kontakt sam po sebi predstavlja sasvim zasebnu kategoriju nelinearnosti. Nastavite da pratite naš vebsajt i društvene mreže kako biste saznali više o ovoj temi u nekom od naših narednih članaka.
Mnogi softveri imaju opciju zadavanja različitih tipova za 1D konačne elemente kao što su “gredni element”, “prost štap”, “rebro” itd. Često se među ovim tipovima mogu naći i elementi koji primaju samo pritisak ili koji primaju samo zatezanje (prost štap efektivan samo za pritisak/zatezanje). Ako je ovo svojstvo dodeljeno elementu, on će apsorbovati samo “željenu” silu. To znači da, ako se druga “neželjena” sila javi u prvoj iteraciji proračuna, u sledećoj iteraciji ovaj element će biti izuzet iz proračuna. Ne treba pobrkati prost štap koji je efektivan samo na zatezanje sa kablom. Iako kablovi ne mogu da prime silu pritiska, te su stoga izloženi samo zatezanju, da bi kablovi mogli da održe stabilnost i da nose opterećenja, prvo ih je potrebno prednapregnuti, odnosno zategnuti pre nanošenja drugih opterećenja. Ovaj slučaj nas vodi nazad u geometrijsku nelinearnost, ali da bismo skratili već poduži tekst, ova vrsta nelinearnosti će biti objašnjenja u nekom od narednih članaka.
Imajući u vidu sve gorepomenuto, može se zaključiti da opisane situacije predstavljaju realno ponašanje konstrukcija i da upotreba nelinearnih MKE proračuna približava naše modele realnosti. Stoga, mi u Tim Global Engineeringu nemamo dilemu oko korišćenja nelinearnih MKE proračuna kad god je potrebno u cilju dobijanja tačnih i pouzdanih rezultata. Ipak, ova vrsta proračuna je veoma zahtevna i može oduzeti dosta vremena. Ostaje na inženjeru da odluči da li je primena ove vrste proračuna opravdana ili ne. Ali, bez obzira na sve, jedno je sigurno – kada se radi o sigurnosti i stabilnosti konstrukcije, ne treba praviti nikakav kompromis.





