NICHTLINEARITÄTEN IN FEM
In unserem vorherigen Artikel haben wir erklärt, wie wir die Finite-Elemente-Methode in der Tragwerksplanung einsetzen können, und sind zu dem Schluss gekommen, dass FEM ein hervorragendes Werkzeug zur Lösung vieler Probleme in diesem, aber auch in vielen anderen Ingenieurbereichen ist. Dieses Mal gehen wir etwas tiefer und sehen uns die Arten von Analysen an, die wir durchführen können.
Die grundlegendste Methode in der FEM ist die lineare Analyse. Und was genau bedeutet „lineare“ Analyse? Wäre die Analyse vollständig linear, wären alle Gleichungen, die die FEM-Software lösen muss, linear und die gewünschten Ergebnisse könnten einfach in einem Schritt aus der gegenseitigen Abhängigkeit der Lasten und der Anfangssteifigkeit des Modells bestimmt werden. Keiner der Faktoren, die diese lineare Beziehung beeinträchtigen könnten, wäre berücksichtigt – Geometrie der Struktur, Materialeigenschaften, nur in eine Richtung wirksame Stützen, deren Teilaktivität usw. In Wirklichkeit verhalten sich Strukturen jedoch nicht linear. Zunächst einmal wirken Lasten nicht „plötzlich“ auf die Struktur ein. Die Strukturelemente werden unter dem Einfluss dieser Belastungen verformt, und diese Verformungen wirken sich weiter auf die zukünftige Umverteilung der Kräfte zwischen den Elementen aus. Die Abhängigkeit von Kräften und Verformungen ist je nach Materialart unterschiedlich. All dies führt uns zu nichtlinearen Berechnungen in FEM.
Wie wirkt sich die Geometrie auf die Analyse aus?
Zunächst erklären wir, wie sich die Geometrie der Struktur auf die Analyse auswirkt. Wie bereits erwähnt, verformen sich Strukturelemente, wenn eine bestimmte Kraft auf sie einwirkt, da diese Elemente nicht vollständig starr sind. Darüber hinaus kennen wir alle die Grundlagen der Mechanik und wie das Drehmoment das Produkt aus Kraft und Abstand vom Bezugspunkt des Objekts ist. Befände sich der Bezugspunkt auf der gleichen Eben wie die Kraft, würde er kein Moment erzeugen, und somit würde die unverformte Struktur nicht von den Momenten der Axialkräfte beeinträchtigt werden. Da wir gesagt haben, dass sich die Strukturen unter Lasteinwirkung immer verformen, würde dies bedeuten, dass es immer Momente gibt, die durch die Einwirkung von Axialkräften erzeugt werden, die sogenannten Momente zweiter Ordnung. Das ist absolut richtig, aber es gibt immer noch bestimmte Situationen, in denen wir sie ignorieren können. Natürlich können wir sie immer berechnen, aber manchmal wird es unnötig sein, weil es keinen signifikanten Einfluss auf weitere Ergebnisse hat. Situationen und Regeln zur Berücksichtigung von Momenten zweiter Ordnung bei der Analyse und Berechnung von Tragwerken sind in den meisten Baunormen wie Eurocode, AISC, Australische Normen usw. beschrieben.
Und wie wirken sich Berechnungen von Momenten zweiter Ordnung auf FEM aus? Der lineare Ansatz für die Berechnung bedeutet, dass die Software nach der Berechnung der belasteten Struktur einfach die Schnittgrößen wie Momente, Scher- und Axialkräfte ermittelt. Außerdem erhalten wir einen Einblick in die endgültigen Verformungen der Struktur, aber diese Verformungen werden sich nicht auf die Erhöhung des Drehmoments auswirken, da die Software alle inneren Kräfte auf das unverformte System berechnet. Wenn wir uns dagegen entscheiden, eine geometrisch nichtlineare Analyse durchzuführen, so erfolgt die Berechnung iterativ. Die Lasten müssen inkrementell aufgebracht werden, sodass wir mit jedem Inkrement einen neuen Verformungswert erhalten, der die Berechnung im nächsten Schritt beeinflusst. Das Programm fährt mit der iterativen Berechnung fort, bis eine stabile Gleichgewichtslage des Systems erreicht ist.
Materialien mit nichtlinearen Eigenschaften
Der nächste Punkt sind die Materialeigenschaften, die wir für den Fall eines Materialmodells für Baustahl beschreiben werden. Stellen wir uns einen Stahlträger vor, der über seine gesamte Länge gleichmäßig belastet wird. Wenn eine Last aufgebracht wird, biegt sich der Träger, und wenn die Last entfernt wird, kehrt der Träger in seine ursprüngliche Form zurück. Natürlich kann davon ausgegangen werden, dass der Träger ab einem gewissen Verformungsgrad seine ursprüngliche Form nicht wiedererlangen kann. Dies geschieht, wenn der Stahl seine Streckgrenze erreicht, wonach er in die plastische Zone seines Arbeitsdiagramms eintritt. Die Fähigkeit, plastische Verformungen zu entwickeln, ist eine der vorteilhaftesten Eigenschaften des Stahls. Wenn wir in unserer Berechnung ein lineares Materialmodell verwenden, kann das Programm die Stahlplastizität nicht verwenden, da sie in diesem Modell einfach nicht vorhanden ist, da wir sie nicht berücksichtigt haben. Sie sind wahrscheinlich damit vertraut, wie die Spannungs-Dehnungs-Kurve für den Stahl aussieht:
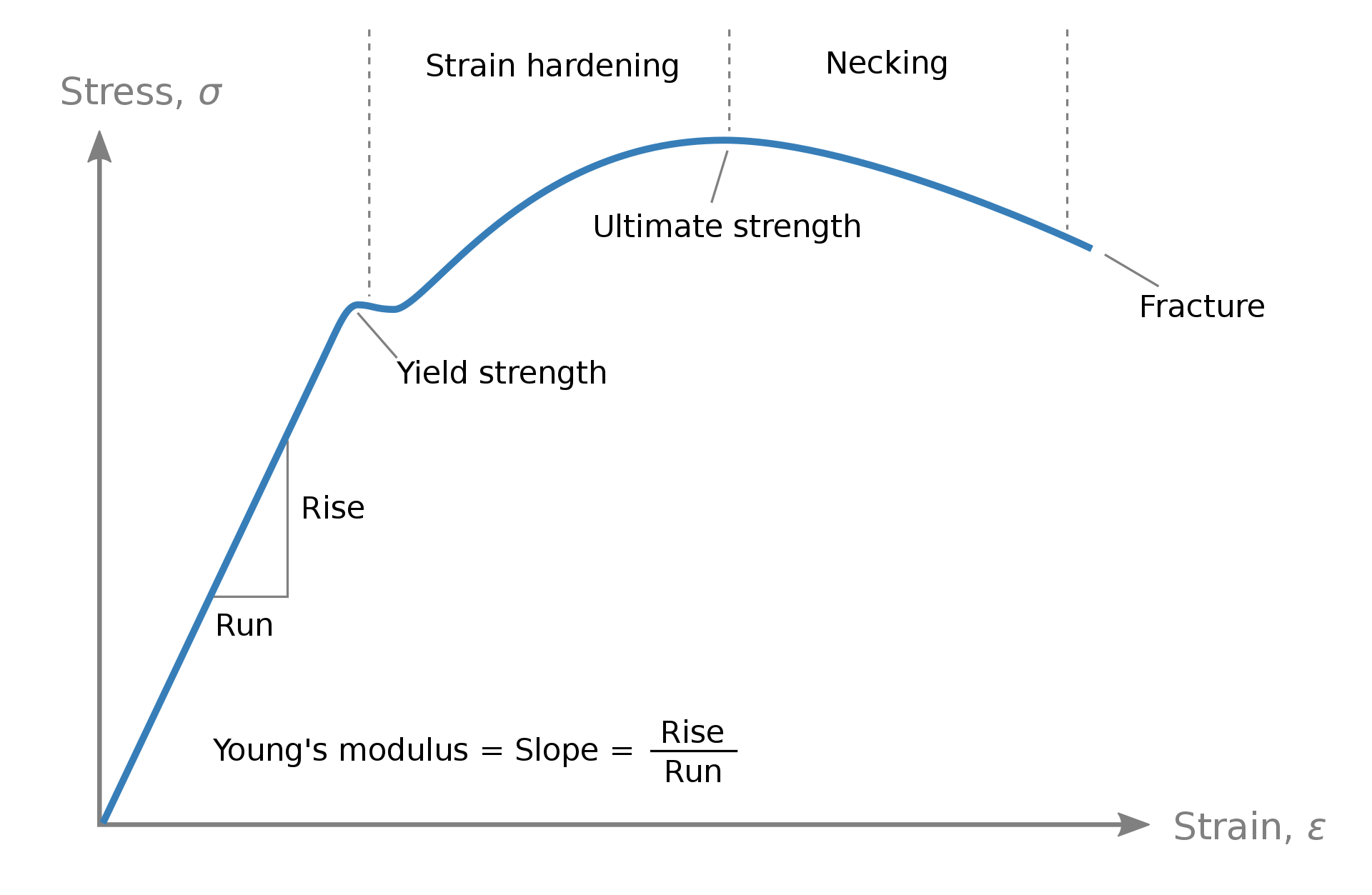
Bei einem linearen Modell entfällt der Teil der Kurve nach der Fließgrenze (plastisches Plateau) – die Kurve ist weiterhin linear in Form einer unendlichen Linie. Das bedeutet, dass bei ständiger Erhöhung der Belastung auch die Spannung linear ansteigen würde und über die Streckgrenze (bis ins Unendliche) gehen könnte. Dies ist natürlich nicht möglich. Wenn die Dehnungen (die sich aus den durch die Belastung der Elemente verursachten Verformungen ergeben) in unserem Modell die plastische Zone erreichen, werden die Spannungen nur geringfügig ansteigen, während der Querschnitt plastisch wird. Wollen wir diese Effekte in unserer Berechnung berücksichtigen, müssen wir ein nichtlineares Materialmodell verwenden. Software berechnet die Dehnungen auf der Grundlage der Verformungen und dann die entsprechenden Spannungen. Wenn die Dehnungen im Diagramm in den plastischen Bereich eintreten, führt jede nachfolgende Belastungserhöhung zu einer weiteren Entwicklung der Dehnung, während die Spannung an der Streckgrenze bleibt (oder etwas höher ist). Natürlich gibt es Einschränkungen für das plastische Dehnungsgrad, die den einschlägigen Normen entnommen werden können. Diese Normen enthalten auch Empfehlungen zur Implementierung eines geeigneten nichtlinearen Materialmodells im FEM-Modell, da die Implementierung der realen Spannungs-Dehnungs-Kurve in der Software sehr anspruchsvoll ist.
Als Tragwerksplaner haben wir erklärt, wie sich die Materialnichtlinearität in der Berechnung von Stahltragwerken widerspiegelt. Es gibt jedoch viele Materialien mit nichtlinearen (elastischen und/oder plastischen) Eigenschaften, deren Verhalten sich stark von dem von Stahl unterscheiden kann. Die Eigenschaften dieser Materialien können der einschlägigen Literatur entnommen oder durch experimentelle Laborversuche ermittelt werden.
Nichtlinearitäten in Bezug auf Auflager und Elementtypen
Nichtlinearitäten können sich schließlich auf Auflagerbedingungen und Elementtypen beziehen. Wir können die Auflager in unserem Modell so platzieren, dass sie gegen Druck oder Zug unwirksam sind, wir können Reibung oder zulässige Verschiebungen (Gleiten) der Auflager einbeziehen. Ein gutes Beispiel für die Unwirksamkeit eines Auflagers ist die Verhinderung der Bewegung der Fundamentplatte in vertikaler Richtung. Der Boden (für die Zwecke dieses Beispiels sei fester Felsboden angenommen) unter dem Fundament verhindert dessen Abwärtsbewegungen (in Richtung der Schwerkraft) und damit die Bewegung des gesamten Tragwerks. Andererseits verhindert der Boden nicht das Anheben des Tragwerks (und kann auch keine Zugkräfte im Kontakt mit dem Fundament übertragen). In diesem Fall wäre die geeignete Art, die Fundamentplatte zu unterstützen, eine Oberflächenunterstützung zu schaffen, die für Spannung (oder für die Hebung) unwirksam ist. Oder stellen Sie sich einen Stahlträger vor, der ohne Verankerung einfach auf zwei Wänden aufliegt. Auch hier haben wir keine Möglichkeit, das Anheben des Trägers zu verhindern, da er nicht an der Wand befestigt ist. Daher müssen wir Stützen an den Enden der Träger erstellen, die durch die erwähnte Nichtlinearität gekennzeichnet sind. Aber wie sieht es mit der horizontalen Bewegung aus? Man könnte sagen, dass der Träger in horizontaler Richtung nicht gestützt wird, aber dank der Reibung haben wir immer noch einen gewissen Bewegungswiderstand. Die Reibung kann den Stützen als Nichtlinearität zugeordnet oder als Eingangsgröße für den Kontakt modelliert werden. Der Kontakt selbst stellt eine völlig eigene Kategorie der Nichtlinearität dar. Folgen Sie weiterhin unserer Website und sozialen Medien, um in einem unserer nächsten Artikel mehr über dieses Thema zu erfahren.
Viele Softwareprogramme haben die Möglichkeit, unterschiedliche Typen für finite 1D-Elemente anzugeben, z. B. „Stabelemente“, „Fachwerk“, „Rippe“ usw. Unter diesen Typen finden Sie häufig auch Elemente, die nur Druck oder nur Zug erhalten (ein einfacher Stab, der nur für Druck/Zug wirksam ist). Wird einem Element diese Eigenschaft zugewiesen, nimmt es nur die „gewünschte“ Kraft auf. Das bedeutet, wenn in der ersten Iteration der Berechnung eine andere „unerwünschte“ Kraft auftritt, wird dieses Element in der nächsten Iteration von der Berechnung ausgeschlossen. Ein einfacher Stab, der nur zum Spannen dient, sollten Sie nicht mit einem Kabel verwechseln. Obwohl die Kabel die Druckkraft nicht aufnehmen können und sind daher nur der Zugspannung ausgesetzt, müssen sie, damit die Kabel ihre Stabilität bewahren und Lasten tragen können, zuerst vorgespannt werden, das heißt, gespannt werden, bevor andere Lasten aufgebracht werden. Dieser Fall führt uns zurück zur geometrischen Nichtlinearität, aber um den ohnehin schon langen Text abzukürzen, wird diese Art der Nichtlinearität in einem der folgenden Artikel erklärt.
Unter Berücksichtigung aller oben genannten Punkte, lässt sich daraus schließen, dass die beschriebenen Situationen das reale Verhalten von Tragwerken darstellen und dass die Verwendung nichtlinearer FEM-Berechnungen unsere Modelle der Realität näher bringt. Daher haben wir bei Tim Global Engineering keine Bedenken, bei Bedarf nichtlineare FEM-Berechnungen einzusetzen, um genaue und zuverlässige Ergebnisse zu erhalten. Diese Art der Berechnung ist jedoch sehr anspruchsvoll und kann sehr zeitaufwändig sein. Die Entscheidung liegt beim Ingenieur, ob die Anwendung dieser Art der Berechnung gerechtfertigt ist oder nicht. Aber eines ist bei allem sicher – wenn es um die Sicherheit und Stabilität des Tragwerks geht, sollten keine Kompromisse gemacht werden.





